티스토리 뷰

https://www.acmicpc.net/problem/17779
17779번: 게리맨더링 2
재현시의 시장 구재현은 지난 몇 년간 게리맨더링을 통해서 자신의 당에게 유리하게 선거구를 획정했다. 견제할 권력이 없어진 구재현은 권력을 매우 부당하게 행사했고, 심지어는 시의 이름도
www.acmicpc.net
이번 문제는 NxN 크기의 인구수들이 주어졌을 때, 주어진 조건에 따른 선거구 인구 수를 계산한 후, 인구가 가장 많은 선거구와 가장 적은 선거구의 인구 차이의 최솟값을 구하는 문제이다. 이 문제는 알고리즘 분류에서도 확인할 수 있듯, 구현과 브루트포스 문제이다. 즉, 일일이 가능한 모든 경우를 검사해야 하기에 굉장히 귀찮은 문제다.
이 문제의 답을 구하기 위해 생각한 문제의 흐름(의사 코드)는 다음과 같다.
- 반복문을 이용해 x, y, d1, d2의 값을 구한다.
- 저 4개의 값에 따른 경계선을 구한다.
- 1번 선거구부터 5번 선거구까지 기록한다.
- 기록한 선거구에 따른 인구수를 계산한다.
- 최대 인구수와 최소 인구수의 차를 계산한 후, 답을 갱신할 수 있다면 갱신한다.
우선, 1번 과정이다. 1번 과정은 반복문을 이용해 x, y, d1, d2의 값을 구하는 과정이다.
for (int d1 = 1; d1 <= N; ++d1)
{
for (int d2 = 1; d2 <= N; ++d2)
{
for (int x = 1; x + d1 + d2 <= N; ++x)
{
for (int y = 1; y + d2 <= N; ++y)
{
for (int r = 0; r < MAX; ++r)
{
for (int c = 0; c < MAX; ++c)
areaIdx[r][c] = 0;
}
bool canCheck = Check(x, y, d1, d2);
if (canCheck)
{
pair<int, int> result = CheckPopulation();
if (answer > result.first - result.second)
answer = result.first - result.second;
}
}
}
}
}x, y, d1, d2는 적어도 1부터 N까지의 값을 가질 수 있기에, 일단은 모든 경우를 다 살펴 보아야 한다. 하지만 문제의 조건에 '(d1, d2 ≥ 1, 1 ≤ x < x + d1 + d2 ≤ N, 1 ≤ y - d1 < y < y + d2 ≤ N)' 라는 조건이 있다. 이를 반복문에 적용하여 반복 횟수를 조금이나마 줄일 수 있다. 4개의 반복문을 통해 가능한 모든 x, y, d1, d2의 값과 이에 따른 결과를 검사한다. 반복문 안의 Check 함수, CheckPopulation 함수 등은 나중에 다시 설명할 것이다.
이제, 경계선을 구하는 2번 과정이다.
int N;
int population[MAX][MAX]; // 문제의 입력으로 주어지는 인구수
int areaIdx[MAX][MAX]; // 선거구 번호를 기록하는 2차원 배열
// 주어진 (r, c)가 유효한 범위 안에 있다면 true를 반환하는 함수
bool IsIn(int r, int c)
{
return 1 <= r && r <= N && 1 <= c && c <= N;
}
bool Check(int x, int y, int d1, int d2)
{
// 경계선의 가장 위, 아래, 오른쪽, 왼쪽의 좌표
int topR = x, topC = y;
int leftR = x + d1, leftC = y - d1;
int rightR = x + d2, rightC = y + d2;
int bottomR = x + d1 + d2, bottomC = y + d2 - d1;
// 경계선이 유효한 범위를 벗어났다면 false를 반환
if (IsIn(topR, topC) == false || IsIn(leftR, leftC) == false || IsIn(rightR, rightC) == false || IsIn(bottomR, bottomC) == false)
return false;
for (int r = topR, c = topC; r <= leftR; ++r, --c)
areaIdx[r][c] = 5;
for (int r = leftR, c = leftC; r <= bottomR; ++r, ++c)
areaIdx[r][c] = 5;
for (int r = bottomR, c = bottomC; c <= rightC; --r, ++c)
areaIdx[r][c] = 5;
for (int r = rightR, c = rightC; c >= topC; --r, --c)
areaIdx[r][c] = 5;
Area1(x + d1 - 1, y);
Area2(x + d2, y + 1);
Area3(x + d1, y - d1 + d2 - 1);
Area4(x + d2 + 1, y - d1 + d2);
Area5(topR, leftC, bottomR, rightC);
return true;
}Check 함수는 x, y, d1, d2의 값에 따른 경계선과 선거구를 결정하는 함수이다. 그리고 1번 과정의 반복문에서 유효하지 않은 x, y, d1, d2를 걸렀다. 하지만 예외가 있을 수 있다고 생각했다. 그렇기에 경계선의 가장 위, 아래, 오른쪽, 왼쪽의 좌표를 구한 후, 이 좌표가 범위 안에 있지 않을 경우 false를 반환해 이 순서를 넘기게 하였다. 그리고 경계선을 그리는데, 경계선은 가장 위에서 왼쪽으로, 왼쪽에서 아래로, 아래에서 오른쪽으로, 오른쪽에서 위로 향하며 그린다. 이를 4개의 반복문으로 구현하였다.
이제 각 선거구를 기록하는 3번 과정이다.
void Area1(int endR, int endC)
{
for (int r = 1; r <= endR; ++r)
{
for (int c = 1; c <= endC && areaIdx[r][c] == 0; ++c)
areaIdx[r][c] = 1;
}
}
void Area2(int endR, int endC)
{
for (int r = 1; r <= endR; ++r)
{
for (int c = N; areaIdx[r][c] == 0; --c)
areaIdx[r][c] = 2;
}
}
void Area3(int endR, int endC)
{
for (int r = N; r >= endR; --r)
{
for (int c = 1; c <= endC && areaIdx[r][c] == 0; ++c)
areaIdx[r][c] = 3;
}
}
void Area4(int endR, int endC)
{
for (int r = N; r >= endR; --r)
{
for (int c = N; c >= endC && areaIdx[r][c] == 0; --c)
areaIdx[r][c] = 4;
}
}
void Area5(int topR, int leftC, int bottomR, int rightC)
{
for (int r = topR; r <= bottomR; ++r)
{
for (int c = leftC; c <= rightC; ++c)
{
if (areaIdx[r][c] == 0)
areaIdx[r][c] = 5;
}
}
}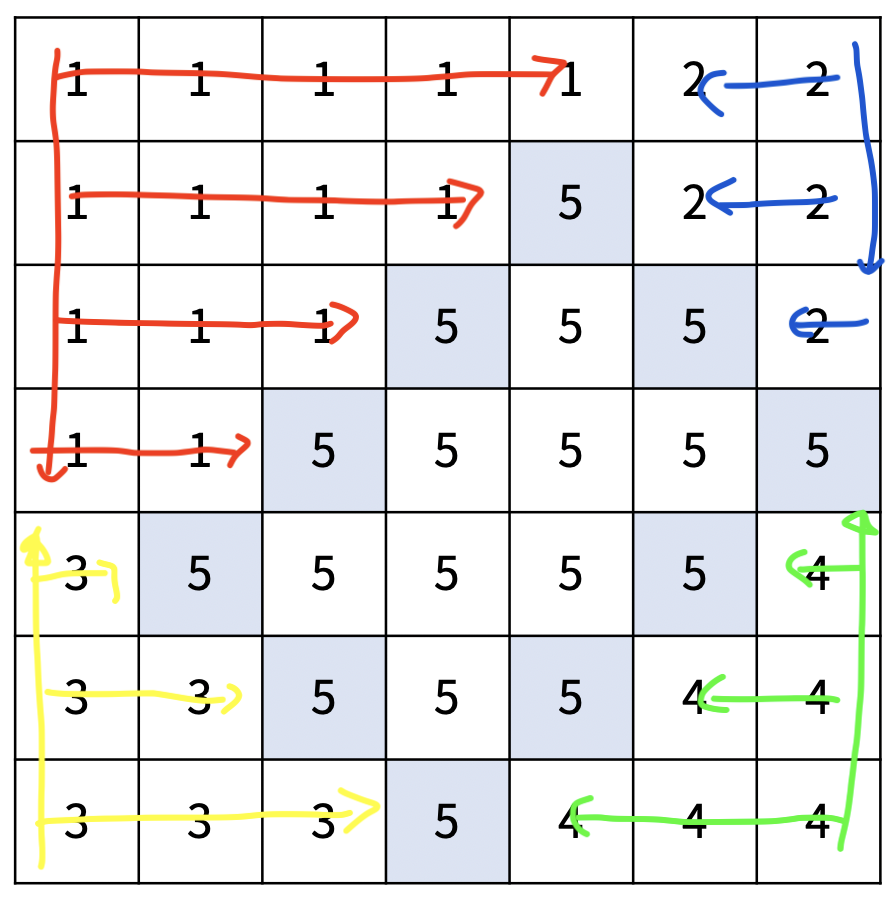
Check 함수에 있었던 Area 함수들이다. Area 뒤의 숫자는 선거구 번호를 나타낸다. 예를 들어, Area1은 1번 선거구를, Area2는 2번 선거구를 구하는 함수이다. 1번부터 4번 선거구는 endR, endC를 인자로 받는다. 그리고 이 값과 기록된 경계선을 기준으로 반복문을 종료할 시점을 정하게 된다. 5번 선거구는 나머지 areaIdx의 값이 0인 구역들을 5번 선거구로 기록하였다.
이제 기록한 선거구에 따른 인구수를 계산하는 4번 과정이다.
pair<int, int> CheckPopulation()
{
int areaPopulation[6] = { 0, 0, 0, 0, 0, 0 };
for (int r = 1; r <= N; ++r)
{
for (int c = 1; c <= N; ++c)
areaPopulation[areaIdx[r][c]] += population[r][c];
}
int maxPopulation = -1;
int minPopulartion = 600000;
for (int i = 1; i <= 5; ++i)
{
maxPopulation = maxPopulation < areaPopulation[i] ? areaPopulation[i] : maxPopulation;
minPopulartion = minPopulartion > areaPopulation[i] ? areaPopulation[i] : minPopulartion;
}
return { maxPopulation, minPopulartion};
}어차피 각 선거구는 int형 숫자이기에, 길이가 6인 areaPopulation 배열을 이용하였다. 그리고 모든 칸을 방문하여 그 칸의 선거구 번호를 이용해 인구수를 areaPopulation[선거구_번호] += 인구[r][c]로 저장하였다. 그리고 최대, 최소 인구수는 각각 maxPopulation, minPopulation이라는 변수에 값을 저장한 후, pair를 이용해 반환하였다.
마지막 5번 과정이다.
if (canCheck)
{
pair<int, int> result = CheckPopulation();
if (answer > result.first - result.second)
answer = result.first - result.second;
}4번 과정에서 pair로 반환한 두 값의 차가 answer보다 크다면 answer를 갱신한다.
다음은 전체 코드이다.
#include <iostream>
#define MAX 21
using namespace std;
int N;
int population[MAX][MAX];
int areaIdx[MAX][MAX];
bool IsIn(int r, int c)
{
return 1 <= r && r <= N && 1 <= c && c <= N;
}
void Area1(int endR, int endC)
{
for (int r = 1; r <= endR; ++r)
{
for (int c = 1; c <= endC && areaIdx[r][c] == 0; ++c)
areaIdx[r][c] = 1;
}
}
void Area2(int endR, int endC)
{
for (int r = 1; r <= endR; ++r)
{
for (int c = N; areaIdx[r][c] == 0; --c)
areaIdx[r][c] = 2;
}
}
void Area3(int endR, int endC)
{
for (int r = N; r >= endR; --r)
{
for (int c = 1; c <= endC && areaIdx[r][c] == 0; ++c)
areaIdx[r][c] = 3;
}
}
void Area4(int endR, int endC)
{
for (int r = N; r >= endR; --r)
{
for (int c = N; c >= endC && areaIdx[r][c] == 0; --c)
areaIdx[r][c] = 4;
}
}
void Area5(int topR, int leftC, int bottomR, int rightC)
{
for (int r = topR; r <= bottomR; ++r)
{
for (int c = leftC; c <= rightC; ++c)
{
if (areaIdx[r][c] == 0)
areaIdx[r][c] = 5;
}
}
}
bool Check(int x, int y, int d1, int d2)
{
int topR = x, topC = y;
int leftR = x + d1, leftC = y - d1;
int rightR = x + d2, rightC = y + d2;
int bottomR = x + d1 + d2, bottomC = y + d2 - d1;
if (IsIn(topR, topC) == false || IsIn(leftR, leftC) == false || IsIn(rightR, rightC) == false || IsIn(bottomR, bottomC) == false)
return false;
for (int r = topR, c = topC; r <= leftR; ++r, --c)
areaIdx[r][c] = 5;
for (int r = leftR, c = leftC; r <= bottomR; ++r, ++c)
areaIdx[r][c] = 5;
for (int r = bottomR, c = bottomC; c <= rightC; --r, ++c)
areaIdx[r][c] = 5;
for (int r = rightR, c = rightC; c >= topC; --r, --c)
areaIdx[r][c] = 5;
Area1(x + d1 - 1, y);
Area2(x + d2, y + 1);
Area3(x + d1, y - d1 + d2 - 1);
Area4(x + d2 + 1, y - d1 + d2);
Area5(topR, leftC, bottomR, rightC);
return true;
}
pair<int, int> CheckPopulation()
{
int areaPopulation[6] = { 0, 0, 0, 0, 0, 0 };
for (int r = 1; r <= N; ++r)
{
for (int c = 1; c <= N; ++c)
areaPopulation[areaIdx[r][c]] += population[r][c];
}
int maxPopulation = -1;
int minPopulartion = 600000;
for (int i = 1; i <= 5; ++i)
{
maxPopulation = maxPopulation < areaPopulation[i] ? areaPopulation[i] : maxPopulation;
minPopulartion = minPopulartion > areaPopulation[i] ? areaPopulation[i] : minPopulartion;
}
return { maxPopulation, minPopulartion};
}
int main()
{
ios_base::sync_with_stdio(0);
std::cout.tie(0);
cin.tie(0);
int answer = 987654321;
cin >> N;
for (int r = 1; r <= N; ++r)
{
for (int c = 1; c <= N; ++c)
cin >> population[r][c];
}
for (int d1 = 1; d1 <= N; ++d1)
{
for (int d2 = 1; d2 <= N; ++d2)
{
for (int x = 1; x + d1 + d2 <= N; ++x)
{
for (int y = 1; y + d2 <= N; ++y)
{
for (int r = 0; r < MAX; ++r)
{
for (int c = 0; c < MAX; ++c)
areaIdx[r][c] = 0;
}
bool canCheck = Check(x, y, d1, d2);
if (canCheck)
{
pair<int, int> result = CheckPopulation();
if (answer > result.first - result.second)
answer = result.first - result.second;
}
}
}
}
}
cout << answer << endl;
return 0;
}'알고리즘 문제' 카테고리의 다른 글
| 프로그래머스 - 삼각 달팽이 (C++) (0) | 2023.08.02 |
|---|---|
| 백준 - Poziome serca (C++) (0) | 2023.07.21 |
| 프로그래머스 - 보행자 천국 (0) | 2023.07.14 |
| 프로그래머스 - 표 편집 (C++) (1) | 2023.06.16 |
| 프로그래머스 - 자물쇠와 열쇠 (C++) (0) | 2023.06.14 |
- Total
- Today
- Yesterday
- 햄버거버튼
- Next.js
- 비트마스킹
- Redux
- 프로그래머스
- react
- 순열
- 타입스크립트
- aws
- C++
- 동적계획법
- 스택
- 카카오맵
- BFS
- 자바스크립트
- 완전탐색
- 리액트
- 코드스테이츠
- SQL
- 넥스트js
- 알고리즘
- 백준
- 다이나믹프로그래밍
- 구현
- 브루트포스
- CSS
- themoviedb
- NextJS
- typescript
- async
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
